使用Python实现一个简单的四则运算解释器
计算功能演示
这里先展示了程序的帮助信息,然后是几个简单的四则运算测试,看起来是没问题了(我可不敢保证,程序没有bug!)。
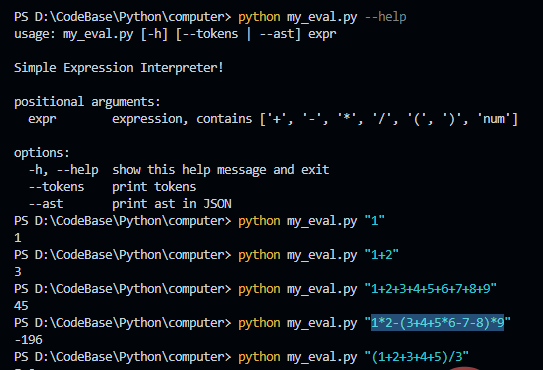
输出 tokens
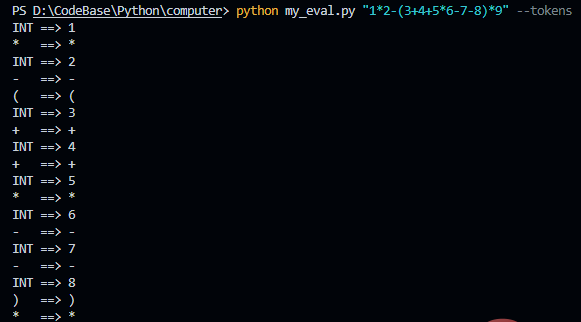
输出 AST
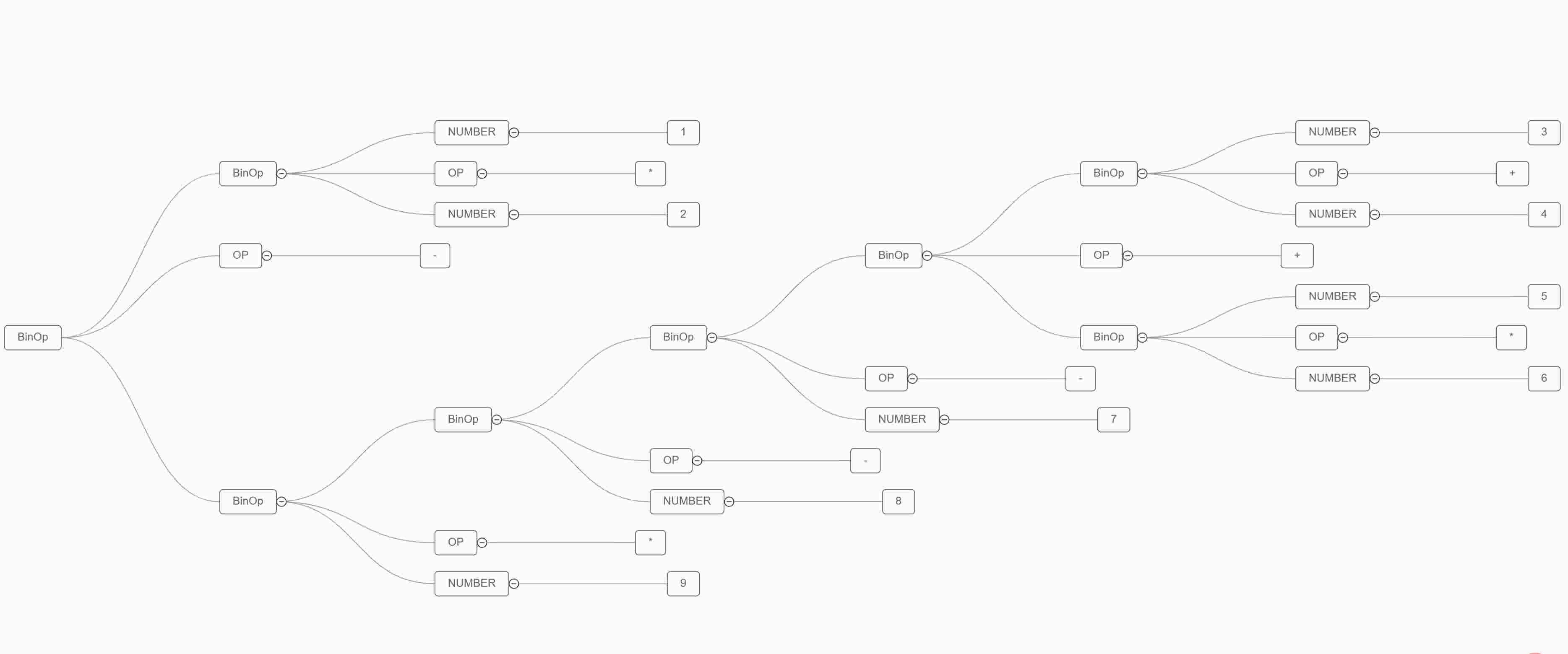
这个格式化的 JSON 信息太长了,不利于直接看到。我们将它渲染出来看最后生成的树形图(方法见前两个博客)。保存下面这个 JSON 在一个文件中,这里我叫做 demo.json,然后执行如下命令:pytm-cli -d LR -i demo.json -o demo.html,然后再浏览器打开生成的 html 文件。
代码
所有的代码都在这里了,只需要一个文件 my_eval.py,想要运行的话,复制、粘贴,然后按照演示的步骤执行即可。
Node、BinOp、Constan 是用来表示节点的类.
Calculator 中 lexizer 方法是进行分词的,本来我是打算使用正则的,如果你看过我前面的博客的话,可以发现我是用的正则来分词的(因为 Python 的官方文档正则表达式中有一个简易的分词程序)。不过我看其他人都是手写的分词,所以我也这样做了,不过感觉并不是很好,很繁琐,而且容易出错。
parse 方法是进行解析的,主要是解析表达式的结构,判断是否符合四则运算的文法,最终生成表达式树(它的 AST)。
"""
Grammar
G -> E
E -> T E'
E' -> '+' T E' | '-' T E' | ɛ
T -> F T'
T' -> '*' F T' | '/' F T' | ɛ
F -> '(' E ')' | num | name
"""
import json
import argparse
class Node:
"""
简单的抽象语法树节点,定义一些需要使用到的具有层次结构的节点
"""
def eval(self) -> float: ... # 节点的计算方法
def visit(self): ... # 节点的访问方法
class BinOp(Node):
"""
BinOp Node
"""
def __init__(self, left, op, right) -> None:
self.left = left
self.op = op
self.right = right
def eval(self) -> float:
if self.op == "+":
return self.left.eval() + self.right.eval()
if self.op == "-":
return self.left.eval() - self.right.eval()
if self.op == "*":
return self.left.eval() * self.right.eval()
if self.op == "/":
return self.left.eval() / self.right.eval()
return 0
def visit(self):
"""
遍历树的各个节点,并生成 JSON 表示
"""
return {
"name": "BinOp",
"children": [
self.left.visit(),
{
"name": "OP",
"children": [
{
"name": self.op
}
]
},
self.right.visit()
]
}
class Constant(Node):
"""
Constant Node
"""
def __init__(self, value) -> None:
self.value = value
def eval(self) -> float:
return self.value
def visit(self):
return {
"name": "NUMBER",
"children": [
{
"name": str(self.value) # 转成字符是因为渲染成图像时,需要该字段为 str
}
]
}
class Calculator:
"""
Simple Expression Parser
"""
def __init__(self, expr) -> None:
self.expr = expr # 输入的表达式
self.parse_end = False # 解析是否结束,默认未结束
self.toks = [] # 解析的 tokens
self.index = 0 # 解析的下标
def lexizer(self):
"""
分词
"""
index = 0
while index < len(self.expr):
ch = self.expr[index]
if ch in [" ", "\r", "\n"]:
index += 1
continue
if '0' <= ch <= '9':
num_str = ch
index += 1
while index < len(self.expr):
n = self.expr[index]
if '0' <= n <= '9':
if ch == '0':
raise Exception("Invalid number!")
num_str = n
index += 1
continue
break
self.toks.append({
"kind": "INT",
"value": int(num_str)
})
elif ch in ['+', '-', '*', '/', '(', ')']:
self.toks.append({
"kind": ch,
"value": ch
})
index += 1
else:
raise Exception("Unkonwn character!")
def get_token(self):
"""
获取当前位置的 token
"""
if 0 <= self.index < len(self.toks):
tok = self.toks[self.index]
return tok
if self.index == len(self.toks): # token解析结束
return {
"kind": "EOF",
"value": "EOF"
}
raise Exception("Encounter Error, invalid index = ", self.index)
def move_token(self):
"""
下标向后移动一位
"""
self.index += 1
def parse(self) -> Node:
"""
G -> E
"""
# 分词
self.lexizer()
# 解析
expr_tree = self.parse_expr()
if self.parse_end:
return expr_tree
else:
raise Exception("Invalid expression!")
def parse_expr(self):
"""
E -> T E'
E' -> + T E' | - T E' | ɛ
"""
# E -> E E'
left = self.parse_term()
# E' -> + T E' | - T E' | ɛ
while True:
tok = self.get_token()
kind = tok["kind"]
value = tok["value"]
if tok["kind"] == "EOF":
# 解析结束的标志
self.parse_end = True
break
if kind in ["+", "-"]:
self.move_token()
left = BinOp(left, value, self.parse_term())
else:
break
return left
def parse_term(self):
"""
T -> F T'
T' -> * F T' | / F T' | ɛ
"""
# T -> F T'
left = self.parse_factor()
# T' -> * F T' | / F T' | ɛ
while True:
tok = self.get_token()
kind = tok["kind"]
value = tok["value"]
if kind in ["*", "/"]:
self.move_token()
right = self.parse_factor()
left = BinOp(left, value, right)
else:
break
return left
def parse_factor(self):
"""
F -> '(' E ')' | num | name
"""
tok = self.get_token()
kind = tok["kind"]
value = tok["value"]
if kind == '(':
self.move_token()
expr_node = self.parse_expr()
if self.get_token()["kind"] != ")":
raise Exception("Encounter Error, expected )!")
self.move_token()
return expr_node
if kind == "INT":
self.move_token()
return Constant(value=value)
raise Exception("Encounter Error, unknown factor: ", kind)
if __name__ == "__main__":
# 添加命令行参数解析器
cmd_parser = argparse.ArgumentParser(
description="Simple Expression Interpreter!")
group = cmd_parser.add_mutually_exclusive_group()
group.add_argument("--tokens", help="print tokens", action="store_true")
group.add_argument("--ast", help="print ast in JSON", action="store_true")
cmd_parser.add_argument(
"expr", help="expression, contains ['+', '-', '*', '/', '(', ')', 'num']")
args = cmd_parser.parse_args()
calculator = Calculator(expr=args.expr)
tree = calculator.parse()
if args.tokens: # 输出 tokens
for t in calculator.toks:
print(f"{t['kind']:3s} ==> {t['value']}")
elif args.ast: # 输出 JSON 表示的 AST
print(json.dumps(tree.visit(), indent=4))
else: # 计算结果
print(tree.eval())总结
本来想在前面说一下为什么叫 my_eval.py,但是感觉看到后面的人不多,那就在这里说好了。如果写了一个复杂的表达式,那么怎么验证是否正确的。这里我们直接利用 Python 这个最完美的解释器就好了,哈哈。这里用 Python 的 eval 函数,你当然是不需要调用这个函数,直接复制计算的表达式即可。我用 eval 函数,只是想表达为什么我的程序会叫 my_eval 这个名字。
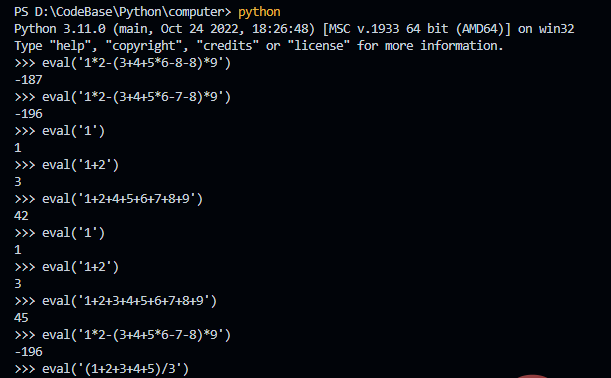
这样实现下来,也算是完成了一个简单的四则运算解释器了。不过,如果你也做一遍的话,也估计会和我一样感觉到整个过程很繁琐。因为分词和语法解析都有现成的工具可以来完成,而且不容易出错,可以大大减少工作量。不过,自己来一遍也是很有必要的,在使用工具之前,至少也要了解工具的作用。
以上就是使用Python实现一个简单的四则运算解释器的详细内容,更多请关注其它相关文章!
