Java怎么用位运算实现乘法运算
十进制相乘
例如,26 * 15,在进行乘法操作时,我们一般这样算,先用5乘以6得到30,把0写下把3记在一边,再用5乘以2得到10再加上之前的3写在下面,得到130;计算完5再计算1分别乘以6和2把得到的结果26记在下面,然后把130和26相加(有错位)得到390。

二进制相乘
看完了十进制的相乘,再来看下二进制的相乘,基本原理是一样的,也是以十字相乘法为例,计算 5 * 7。
5的二进制为101,7的二进制为111,来看下二进制的十字相乘法。
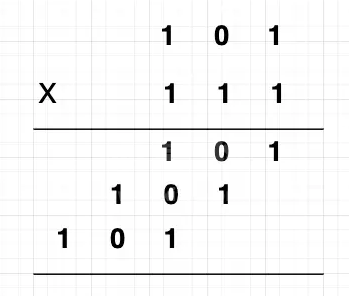
可以看到二进制为101和二进制111用传统的方式来计算,得到的结果为100011,而二进制100011对应的十进制为35。
所以说,在计算的过程中,十进制和二进制的计算方式是一样的,当然这里就不进行举例和证明了。
思路分析
既然计算过程有了,那么怎么样用代码来实现呢?
我们再来看下上图中二进制的计算过程:
先用二进制
111的最后一位1乘上101得到101。再用二进制
111的倒数第2位1乘上101得到101。再用二进制
111的倒数第3位1乘上101得到101。得到的三个
101进行二进制相加,得到100011。
注意,第2步和第3步得到的结果101都往前挪了一位,相当于1010和10100,也就是最后相加的计算为:10100 + 1010 + 101 = 100011。
再来看得到最终相加的计算10100 + 1010 + 101 = 100011,也就是只要我们找到如何把数据转换为几位数的相加就可以了,因为之前已经实现了如何用位运算实现加法操作。
这三个数101、1010、10100的数量刚好与二进制111的个数相同,也就是二进制(上图下面那个乘数111)有几位就会产生几个数相加,如果是与11111相乘就会产生5个数相加。
再来看数据之前的关系:
第一次相乘结果:
101 = 101 + 0第二次相乘结果:
1111 = 101 < 1 + 101 = 1010 + 101第三次相乘结果:
100011 = 101 < 2 + 1111 = 10100 + 1010 + 101
从这里我们可以看到,每计算一次,101只需要向左移一次再加上上一次的计算结果就可以了。
那么,怎么知道要左移多少次呢?从这里例子中看,111每次计算后,向右移动一次,101也跟着向左移动一次,直到111只剩最后一位,则停止计算就好了。
代码实现
根据上面的思路,来实现一下代码:
// 用位运算实现加法
public static int add(int a, int b) {
int sum = 0;
while (b != 0) {
sum = a ^ b;
b = (a & b) << 1;
a = sum;
}
return sum;
}
// 用位运算实现减法
public static int multi(int a, int b) {
int res = 0;
while (b != 0) {
if ((b & 1) != 0) {
res = add(res, a);
}
a <<= 1;
b >>>= 1;
}
return res;
}运行一下代码,看下结果:
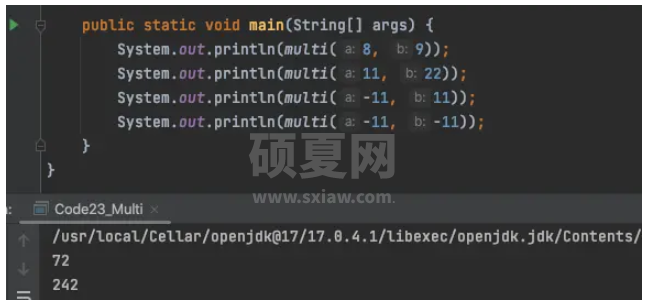
可以看到计算是正确的,而且还支持负数。
以上就是Java怎么用位运算实现乘法运算的详细内容,更多请关注其它相关文章!
