偷偷看了点计算机基础,从此学Java犹如开挂!
学习Java之前,我想问一个问题,你们觉得有没有必要学习计算机基础?
很多人觉得没有必要看那些枯燥晦涩的基础知识,还不如直接从HelloWorld开始,先接触程序,有个印象,代码跑起来,然后再逐步深入学习程序的语法,到最后使用程序搭建项目,也就是实战学习法。
首先我不否定这样的学习方式,确实对某部分同学来说是比较适用的,尤其是一些着急找工作的同学,先学会怎么去用,至于原理,可以以后慢慢去深入了解,毕竟没有什么比面包?更重要。
但是对于我们大对数从头开始学习的同学,我还是建议从计算机的一些基础小知识开始,了解程序设计的思想和常识,这对于我们以后的学习也是非常有帮助的。就好比盖房子,有的人盖的是茅草屋,有的人盖的是泥瓦屋,而有人却想着盖二层小洋楼。基础的深浅程度,直接决定了以后成就的高低。
那么现在我们就来简单了解下计算机的一些基础小知识。
一. 机器语言的分类
机器语言
机器语言就是计算机能直接能识别的语言,它是直接用二进制代码指令表达的计算机语言。它是由一串0和1组成的代码,有一定的位数,并分成若干段,各段的编码表示不同的含义。例如下面就是一串简单的机器码:
010100100000 // 520
那么很多人问,为什么机器码是0和1组成的?
因为机器码需要控制电脑硬件对程序指令做出响应,0代表低电位,1代表高电位,这样才能产生逻辑电路,就相当于控制开关一样,0是关闭,1是打开。
汇编语言
汇编语言是一种面向开发人员的语言,由于机器语言都是0和1,开发人员难以直接操控和使用,那么就需要使用一些特殊的符号作为二进制码的标记,开发人员通过输入这些特殊的符号来完成指令下发,让电脑为我们工作,这些特殊的符号就是汇编语言。计算机不能直接识别汇编语言,需要用一种软件将汇编语言翻译成机器语言。它与机器语言的区别在于指令的表示方法上,汇编语言的主体是汇编指令,相比于机器指令,编程人员更容易记住。
MOV AX,1234H //汇编指令: 寄存器AX的内容送到1234H中 101110000011010000010010 //机器指令
高级语言
高级语言常见如:c,c++,java,python,php等等。
它更接近于我们平时正常的人思维,其最大的特点是编写容易,代码可读性好。实现同样的功能,使用高级语言耗时更少,程序代码量更短,更容易阅读。其次,高级语言是可移植的,也就是说,仅需稍作修改甚至不用修改,就可将一段代码运行在不同类型的计算机上。
print('Hello World') // python版HelloWorld我们从这个程序可以看出来,高级语言屏蔽了机器内部指令运行细节,我们可以像写作一样书写程序,而不用关心语言内部的实现细节,这大大提高了我们的开发效率,节约开发成本。
当然,其缺点也很明显,使用高级语言编写的程序运行时,需要先将其翻译成低级语言计算机才能运行它,在翻译过程中可能会产生一些多余的部分,运行效率低些。另外,对硬件的可控性相对于低级语言弱些,目标代码量较大。
二. 进制
推荐使用在线工具进行进制转换:
https://tool.oschina.net/hexconvert/
二进制
由数字0和1组成,逢二进一,比如机器码就是二进制的,是最简单的计算机可读懂的代码,例如 0101(表示十进制数字5)。
八进制
由1到7组成的数字串,数字最大不会超过7,逢八进一,例如 157(表示十进制数字111)
十进制
我们日常使用的数字都是十进制类型的,逢十进一,例如 0123456789。
十六进制
由1到9,a-f(或者是A-F,分别代表10-15)组成的数字串,数字最大不会超过15,其中字母是不区分大小写的,逢十六进一,例如0F83(表示十进制数3971)
进制转换
1. K进制与十进制数的转换
假设有一个n+1位的K进制数,它的形式如下:
AnAn-1…A3A2A1A0
则它的大小为:(也就是对应的我们能看懂的十进制数为)
A0 * K^0 + A1 * K^1....+ An * K^n //K^n表示K的n次方
二进制数:10101 转换成 十进制数为:21
1*2^4 + 0*2^3 + 1*2^2 + 0*2^1+1*2^0 = 21
2. 十进制与k进制的转换
短除法。
举个栗子:
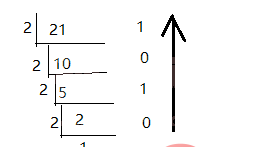
从图可以看出,用十进制数21一直除以2,每次得到的余数倒数就是最后的二进制数10101。同样,十进制转八进制、十进制转十六进制都是一样的套路,非常简单。
3. 二进制与八进制和十六进制之间转换
8是2的3次方,16是2的4次方,所以这之间的转换存在一种快捷方法。以2转8示例,将2进制从低位到高位,每3个一组,如果是十六进制就每4个一组,高位不足3位的补0,然后将每组依次转换成对应的十进制,得到的结果就是对应的8进制或者16进制。
二进制10101100101转八进制:2545
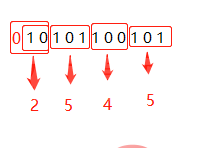
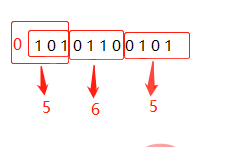
二进制10101100101转十六进制:565
三. 原码、反码、补码
在计算机中,最小的单位是位,也称为比特(bit)。而另一个常用单位是字节,一个字节是8位,也就是8比特,所以我们常用的二进制表示法是8位。
原码
原码是一种非常常见的二进制表示形式。在原码中,为了区别正数和负数,将二进制中的最高位作为符号位,如果是0表示正数,如果是1表示负数。
举个栗子:
0000 0001 // 表示 1 1000 0001 // 表示 -1
反码
不知道大家有没有注意到原码的一个问题,那就是负数参与计算的时候,比如
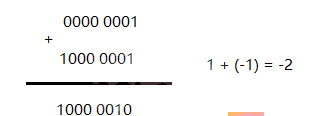
出现了一个大问题,就是1 + (-1) 不等于0,而等于 -2。
这可咋整?
为了解决这个问题,聪明的计算机前辈们想到了反码。原码转反码的规则为:正数的反码为其本身,负数的反码是符号位不变,其他位取反。取反的规则就是如果是0就变成1,如果是1就变成0。
我们来看下转成反码的计算:
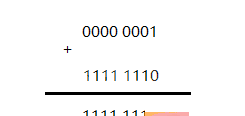
得到的结果是1111 1111。
哎?这不对啊,怎么不是0?
别急,这只是反码的计算结果,我们将反码转成原码 1111 1111 —> 1000 0000,得到 -0, 也就是0,完全符合预期的结果,也解决了原码的计算问题。
补码
反码解决了负数计算的问题,但是还有一个问题没有解决,就是 -0 。由于负数最高位的符号位的存在,导致原本八位的二进制数能表示2的8次方即256个数字,使用原码与反码却只能表示255个,这对于我们来说是非常难受的,那么这少的一个数怎么弥补上呢?
秃头的程序员老哥哥们也想出了对应的解决办法——补码。
原码转补码的规则:正数的补码就是其本身,负数的补码是符号位不变,其余位数取反(即变成反码)再加1。
举个栗子:
原码:0000 0001 , 补码:0000 0001
原码:1000 0001 , 补码:1111 1111
计算一下:

从上面看出,利用补码计算我们得到了 0 (而不是 -0 ),解决了少一个数字的问题。
在补码中,规定了0的表示为0000 0000,而1000 0000表示的为-128,注意,这是规定。
注意事项
反码与补码不能直接使用二进制转十进制的规则,转成对应的十进制得到对应的大小,应该先转成原码后才可以。也就是说原码才是直接与大小进行关联的一种表现形式
在计算机系统中,数值一律用补码的形式进行表示与存储
正数的原码、反码与补码都是一样的
负数原转反:符号位不变,其余位取反
负数原转补:符号位不变,其余位取反后加一
负数补转反:符号位不变,其余位减一
负数补转原:符号位不变,其余位减一后取反
以上就是偷偷看了点计算机基础,从此学Java犹如开挂!的详细内容,更多请关注其它相关文章!
