用C++实现最短路径之Dijkstra算法
网络层的链路状态路由选择算法(LS算法),其中一种就是用Dijkstra算法写的。《算法导论》的介绍:Dijkstra算法解决的是带权重的有向图上单源最短路径问题,该算法要求所有边的权重都为非负值。
算法思路
- G集表示所有点集,S集表示已经求解出源到某点的最短路径的点集,V集表示为求出最短路径的点集
- 首先令S=Ø,V=G
如图所示6个点8条边 V={1,2,3,4,5,6}
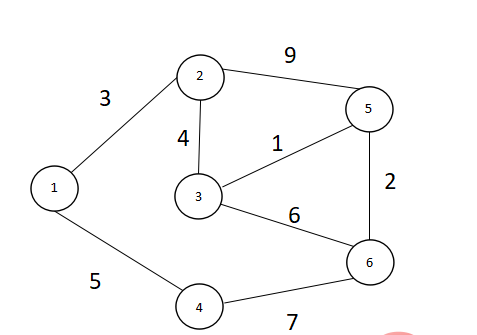
- 取u=1,把点1放入S中,S={1} ,V={2,3,4,5,6},遍历与点1相连的点,并把权值放入数组
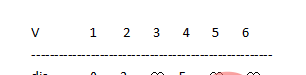
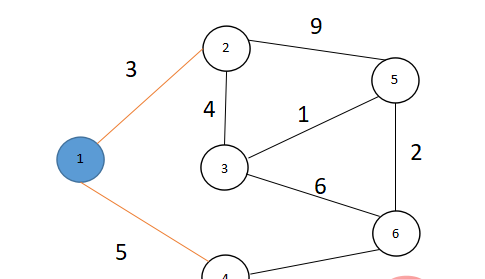
4.由路径数组可得知此时V集中 点2有最短路径(值为3)所以令u=2,则S={1,2} ,V={3,4,5,6}
因为dis[3]=dis[2]+4 ⇒ 7=3+4
… . dis[5]=dis[2]+9 ⇒ 12=3+9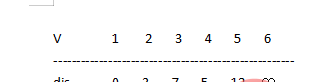
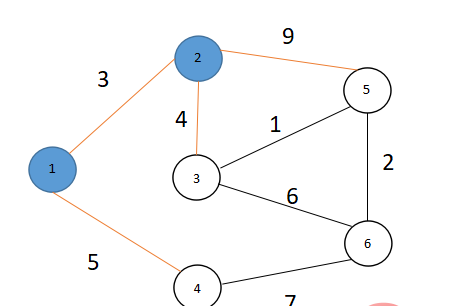
- 同理如今S={1,2},V={3,4,5,6},在V中发现dis[3]为除dis[1],dis[2]外的最小值,所以令S=S∪{3}
此时S={1,2,3},V={4,5,6}
因为dis[5]=12>dis[3]+1=7+1 ⇒ 令 dis[5]=dis[3]+1=7+1=8
因为dis[6]=∞ >dis[3]+6=7+6 ⇒ 令 dis[6]=dis[6]+6=7+6=13
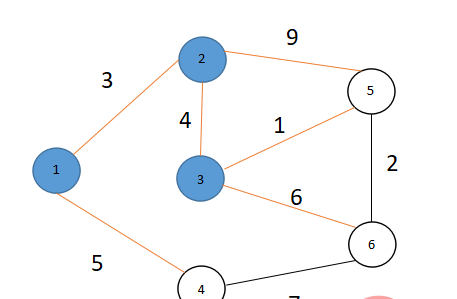
- 同理如今S={1,2,3},V={4,5,6},在V中发现dis[4]为除dis[1],dis[2],dis[3]外的最小值,所以令S=S∪{4}
此时S={1,2,3,4},V={5,6}
因为dis[6]=13>dis[4]+7=5+7 ⇒ 令 dis[6]=dis[4]+7=5+7=12
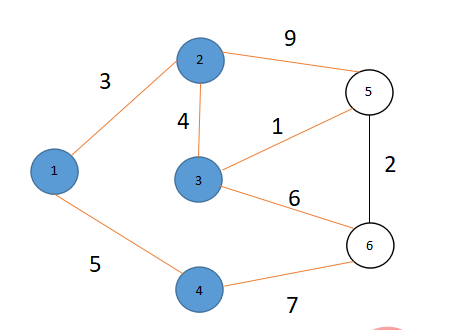
- 同理如今S={1,2,3,4},V={5,6},在V中发现dis[5]为除dis[1],dis[2],dis[3],dis[4]外的最小值,所以令S=S∪{5}
此时S={1,2,3,4,5},V={6}
因为dis[6]=12>dis[5]+2=8+2 ⇒ 令 dis[6]=dis[5]+2=8+2=10
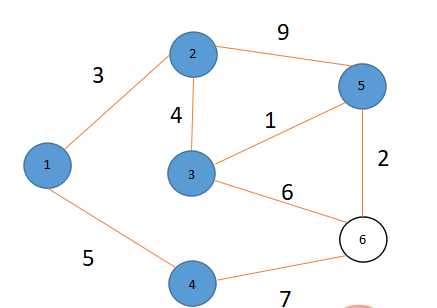
如上从点1到各个点的最短路径就求出来,感觉最近写的很乱,不容易看懂。不过感谢各位看官能够看到这儿。
关于n点m条边求最短路径,一般迭代n次就能得出所有点的最短路径。
现在就是贴出代码惹
/* * @author Wenpupil * @time 2019-04-04 * @version 1.0 * @Description 最短路径之Dijkstra算法 关于无负权的无向图练习 */ #include<iostream> #include<cmath> #include<string.h> #define INIT 9999 using namespace std; int map[20][20]; //存储19个点的无向图 int s[20]; //标记数组 int dis[20]; void mDijkstra(int i,int m) { for(int i=0;i<20;i++) dis[i]=INIT; //初始化dis数组 任务9999为路径无穷大 memset(s,0,20); //初始化标记数组 dis[1]=0; //从1出发自身权为0 for(int i=1;i<=m;i++) //m个点 进行m次迭代 可以得到第m个点的最短路径 { int weightSum=INIT; int u=0; for(int j=1;j<=m;j++) { if(!s[j]&&dis[j]<weightSum) { weightSum=dis[j]; u=j; } } s[u]=1; for(int j=1;j<=m;j++) { if(!s[j]&&map[u][j]>0){ dis[j]=min(dis[j],dis[u]+map[u][j]); } } } } int main(void) { int m,n; //共有m个点,n条边 cin>>m>>n; for(int i=0;i<n;i++) { int x,y,z; //点X和点Y相连 之间权重为Z cin>>x>>y>>z; map[x][y]=map[y][x]=z; } mDijkstra(1,m); //从节点1出发 遍历全图 for(int i=1;i<=m;i++) cout<<dis[i]<<' '; //显示结果 return 0; }
【推荐课程:C++视频教程】
以上就是用C++实现最短路径之Dijkstra算法的详细内容,更多请关注其它相关文章!
