浅谈浮点数运算为什么会产生误差

本篇文章以Python为例，来谈谈为什么浮点数运算会产生误差？介绍一下什么情况下会产生误差？以及如何解决？希望对你们有所助。

【相关推荐：Python3视频教程 】

大家在写代码时都会遇到所谓的浮点误差，如果你还没踩过浮点误差的坑，只能说你太幸运了。

以下图的 Python 为例， 0.1 + 0.2 并不等于 0.3，8.7 / 10 也不等于 0.87，而是 0.869999…，真是太奇怪了

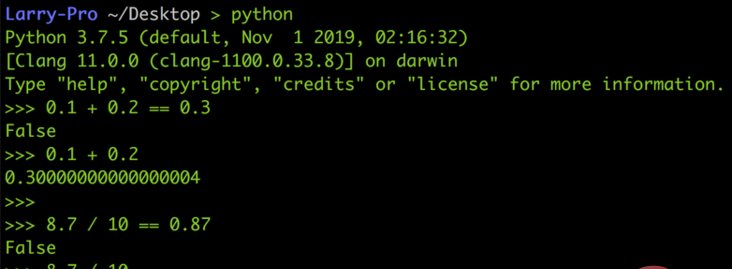
但这绝对不是什么阴间 bug，也不是 Python 设计得有问题，而是浮点数在做运算时必然的结果，所以即便是在 JavaScript 或其他语言中也都是一样：

电脑是怎样储存一个整数的(Integer)

在讲为什么会存在浮点误差之前，先来谈谈电脑是怎么用 0 跟 1 来表示一个 整数 的，大家应该都知道二进制：例如 101 代表 $2^2 + 2^0$ 也就是 5、1010 代表 $2^3 + 2^1$ 也就是 10。

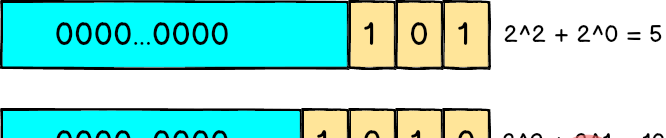
如果是一个无符号的 32 bit 整数，代表它有 32 个位置可以放 0 或 1，所以最小值就是 0000...0000 也就是 0，而最大值 1111...1111 代表 $2^{31} + 2^{30} + ... + 2^1 + 2^0$ 也就是 4294967295

从排列组合的角度来看，因为每一个 bit 位都可以是 0 或 1，整个变量的值有 $2^{32}$ 种可能，所以可以 精确的 表达出 0 到 $2^{23} - 1$ 之间的任一个值，不会有任何误差。

浮点数(Floating Point)

虽然从 0 到 $2^{23} - 1$ 之间存在很多个整数，但其数量终究是 有限 的，就是 $2^{32}$ 那么多个而已；但浮点数就不同了，我们可以这样想：在 1 到 10 这个区间中只有十个整数，却有 无穷多个 浮点数，例如 5.1、5.11、5.111 等等，怎么也列举不完。

但因为在 32 bit 的空间中就只有 2³² 种可能性，为了把所有浮点数都塞在这个 32 bit 的空间里面，许多 CPU 厂商发明了各种浮点数的表示方式，但如果每家 CPU 的格式都不一样也很麻烦，所以最后是以 IEEE 发布的 IEEE 754 作为通用的浮点数运算标准，现在的 CPU 也都遵循这个标准进行设计。

IEEE 754

IEEE 754 里面定义了很多东西，其中包括单精度（32 bit）、双精度（64 bit）和特殊值（无穷大、NaN）的表示方式等等

规格化

以 8.5 这个浮点数来说，如果要变成 IEEE 754 格式的话必须先做一些规格化处理：把 8.5 拆成 8 + 0.5 也就是 $2^3 + (\cfrac{1}{2})^1$ ，接着写成二进位变成 1000.1，最后再写成 $1.0001 \times 2^3$，与十进制的科学记数法很相似。

单精度浮点数

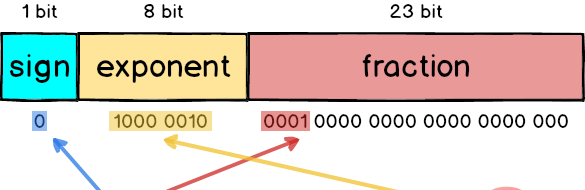
在 IEEE 754 中 32 bit 浮点数被拆分成三个部分，分别是 数符（sign）、阶码（exponent） 和尾数（fraction），加起来总共是 32 个 bit

• 数符（sign）：最左侧的 1 bit 代表正负号，正数的话 sign 就为 0，反之则是 1
• 阶码（exponent）：中间的 8 bit 代表规格化之后的次方数，采用的是 阶码真值 +127 的格式，也就是 3 还要再加上 127 等于 130
• 尾数（fraction）：最右侧的 23 bit 放的是小数部分，以 1.0001 来说就是去掉 1. 之后的 0001

所以如果把 8.5 表示成 32 bit 格式的话应该是这样：

什么情况下会产生误差？

前面举的 8.5 的例子可以表示为 $2^3 + (\cfrac{1}{2})^1$ ，是因为 8 和 0.5 刚好都是 2 的次方数，所以完全不会产生任何精准度问题。

但如果是 8.9 的话因为没办法换成 2 的次方数相加，所以最后会被迫表示成 $1.0001110011… \times 2^3$，而且还会产生大概 $0.0000003$ 的误差，如果对结果好奇的话可以到 IEEE-754 Floating Point Converter 网站上玩玩看。

双精度浮点数

前面所讲的单精度浮点数只用了 32 bit 来表示，为了让误差更小，IEEE 754 也定义了如何用 64 bit 来表示浮点数，跟 32 bit 比起来 fraction 部分扩大了两倍多，从 23 bit 变成 52 bit，所以精准度自然会提高许多。

以刚才的 8.9 为例，用 64 bit 表示的话虽然可以变得更准，但因为 8.9 无法完全写成 2 的次方数相加，到了小数下 16 位仍然会出现误差，不过与单精度的误差 0.0000003 比起来已经小了很多

类似的情况还有像 Python 中的 1.0 跟 0.999...999 是相等的、123 跟 122.999...999 也是相等的，因为他们之间的差距已经小到无法放在 fraction 里面，所以从二进制格式看来它们每一个二进制位都是一样的。

解决方法

既然浮点数的误差是无法避免的，那就只好跟它共处了，下面是两个比较常见的处理方法：

设定最大允许误差 ε (epsilon)

在某些语言会提供所谓的 epsilon，用来让你判断是不是在浮点误差的允许范围内，以 Python 来说 epsilon 的值大约是 $2.2e^{-16}$

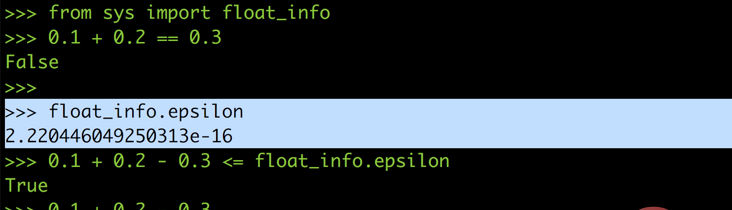
所以你可以把 0.1 + 0.2 == 0.3 改写成 0.1 + 0.2 — 0.3 <= epsilon，这样就能避免浮点误差在运算过程中捣乱，正确的比较出 0.1 加 0.2 是不是等于 0.3 了。

当然如果系统没提供的话你也可以自己定义一个 epsilon，设定在 2 的 -15 次方左右

完全使用十进制进行计算

之所以会有浮点误差，是因为把十进制转为二进制的过程中没办法把所有的小数部分都塞进了尾数中，既然转换可能会有误差，那干脆就不转了，直接用十进制来做运算。

在 Python 里面有一个 module 叫做 decimal，在 JavaScript 中也有类似的包。它可以帮你用十进制来进行计算，就像你自己用纸笔计算 0.1 + 0.2 绝对不会出错、也不会有任何误差。

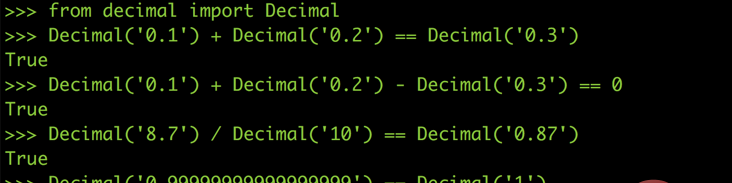
虽然用十进制进行计算可以完全避免浮点数的误差，但因为 Decimal 的十进制计算是模拟出来的，在最底层的 CPU 电路中还是在用二进制进行运算，执行起来会比原生的浮点运算慢很多，所以不建议所有的浮点运算都用 Decimal 来进行。

更多编程相关知识，请访问：编程入门！！

以上就是浅谈浮点数运算为什么会产生误差的详细内容，更多请关注其它相关文章！